13. Introduction to GPU computing with CUDA¶

How GPU computing works
NVIDIA hardware and CUDA
Host and Device parts of code
Threads, blocks, warps, SIMT
GPU memory management
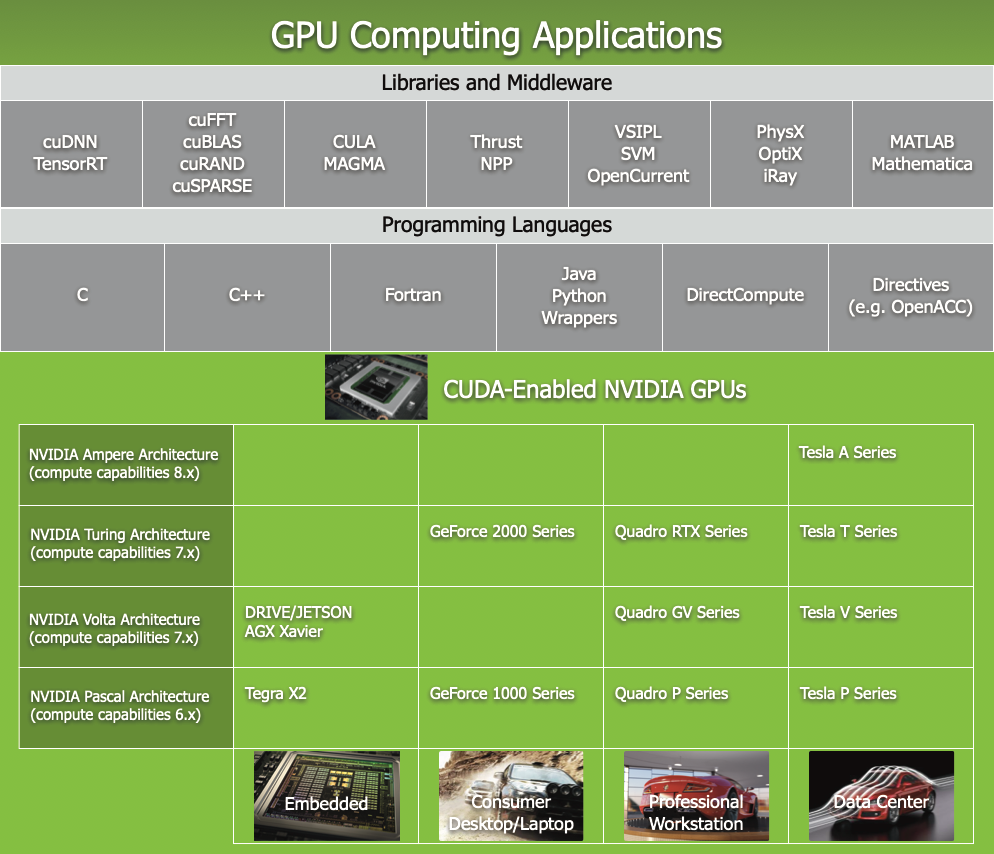
High level applications and CUDA
Pycuda to call CUDA from python
Jupyter note for python scripts

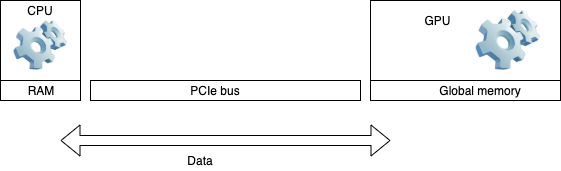
13.1. HOW GPU accelerated computing works¶

Application runs essentially on a CPU
Some procedures can run on GPU
Data is sent back and forth between the devices over PCIe bus
CPU and GPU run cycles independently

13.2. Type of compute tasks to run on GPU¶

Single Instruction Multiple Data (SIMD) simulations can efficiently run across many light weight threads on GPU Stream Multiprocessors.

For example, vector sum:

_images/Single_instruction_multiple_data.png

13.3. Applications runnable on GPU¶

13.4. GPU computing cons and pros¶

Two types of programming environments: CUDA and OpenAcc (less performance efficient).

Pros:

computing power for Single Instruction Multiple Data tasks thanks to available many GPU threads.
Many applications are already developed and ported into CUDA: Matlab, Comsol, VASP, python wrappers (pycuda).

Cons:

Not beneficial for non SIMD computing.
Nontrivial programming in CUDA.
Hardware - CUDA compatibility and dependency on Nvidia support. Relatively old GPU hardware is no longer supported by latest CUDA releases.

13.5. Host and Device parts of a code¶

Data is initialized and may be computed on the CPU (host part)
CPU calls to allocate memory space for DATA on GPU (host part)
CPU sends data to the GPU (host part)
CPU invokes GPU part of the code, kernel, to execute (device part)
GPU executes its code (device part)
CPU receives data from GPU (host part)

Example: hello.cu, without data send/receive. The global is the device directive

#include<stdio.h> 
#include<stdlib.h>

//Kernel definition (device part):
   __global__ void print_from_gpu(void) {
       printf("Hello World! from thread [%d,%d]From device\n", threadIdx.x,blockIdx.x);
}

//Host part:
int main(void) {
       printf("Hello World from host!\n");
    // Kernel invocation with 2 threads
       print_from_gpu<<<1,2>>>();
       cudaDeviceSynchronize();
       return 0;
}

Example: vector_add.cu code snipped with data send/receive:

// Device code
__global__ void VecAdd(float* A, float* B, float* C, int N)
{
    int i = blockDim.x * blockIdx.x + threadIdx.x;
    if (i < N)
        C[i] = A[i] + B[i];
}
            
// Host code
int main()
{
    int N = ...;
    size_t size = N * sizeof(float);

    // Allocate input vectors h_A and h_B in host memory
    float* h_A = (float*)malloc(size);
    float* h_B = (float*)malloc(size);

    // Initialize input vectors
    ...

    // Allocate vectors in device memory
    float* d_A;
    cudaMalloc(&d_A, size);
    float* d_B;
    cudaMalloc(&d_B, size);
    float* d_C;
    cudaMalloc(&d_C, size);

    // Copy vectors from host memory to device memory
    cudaMemcpy(d_A, h_A, size, cudaMemcpyHostToDevice);
    cudaMemcpy(d_B, h_B, size, cudaMemcpyHostToDevice);

    // Invoke kernel
    int threadsPerBlock = 256;
    int blocksPerGrid = (N + threadsPerBlock - 1) / threadsPerBlock;
    VecAdd<<<blocksPerGrid, threadsPerBlock>>>(d_A, d_B, d_C, N);

    // Copy result from device memory to host memory
    // h_C contains the result in host memory
    cudaMemcpy(h_C, d_C, size, cudaMemcpyDeviceToHost);

    // Free device memory
    cudaFree(d_A);
    cudaFree(d_B);
    cudaFree(d_C);
            
    // Free host memory
    ...
}

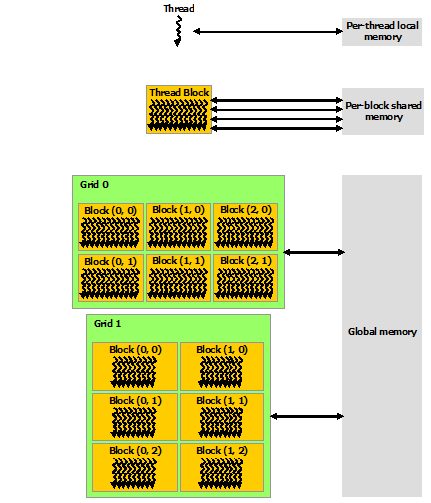
13.6. Threads, blocks, warps, and grid¶

Single computing operation on GPU is done by a thread.
Threads are grouped into a block.
The number of threads in a block is defined by the code developer.
Each block performs the same operation on all its threads.
CUDA employs a Single Instruction Multiple Thread (SIMT) architecture to manage and execute threads in groups of 32 called warps.
Data for each thread may be different.
The blocks are scheduled and run independently of each other.
Blocks are organized into a one-dimensional, two-dimensional, or three-dimensional grid of thread blocks.

13.7. Blocks on Streaming Multiprocessors (SM)¶

A GPU with more multiprocessors will automatically execute the program in less time than a GPU with fewer multiprocessors.

13.8. Thread indexing¶

Each thread in the grid is uniquely identified by its index, ix.
There is also the thread index within a block, threadIdx.x.
Each block within the grid can be identified by its own index, blockIdx.x
The relationship between the indexes:

int i = blockIdx.x * blockDim.x + threadIdx.x;

where blockDim.x is the size of the block.

For convenience of computing multi-dimensional data, the indexes can be defined as one-dimensional, two-dimensional, or three-dimensional:

int ix = blockIdx.x * blockDim.x + threadIdx.x;
int iy = blockIdx.y * blockDim.y + threadIdx.y;
int iz = blockIdx.z * blockDim.z + threadIdx.z;

13.9. Memory Hierarchy¶

CUDA threads may access data from multiple memory spaces during their execution.
Each thread has private local memory.
Each thread block has shared memory visible to all threads of the block and with the same lifetime as the block.
All threads have access to the same global memory.
Data from the host arrives into and departs from the global memory. The global memory is much slower than the other two.
There are also two additional read-only memory spaces accessible by all threads: the constant and texture memory spaces.

13.10. The main challenge in CUDA computing is memory management¶

Data from the host arrives into the global memory, the slowest type of memory on th GPU.
One should avoid using the global memory for thread computing. Copy data into the shared memory, compute, then copy results back into the global memory.
Another challenge often happens due to noncalescent data alignment in global memory. Data is read in warps of size 32. For unstructured data, it may take multiple warp cycles to load the data into the shared memory.

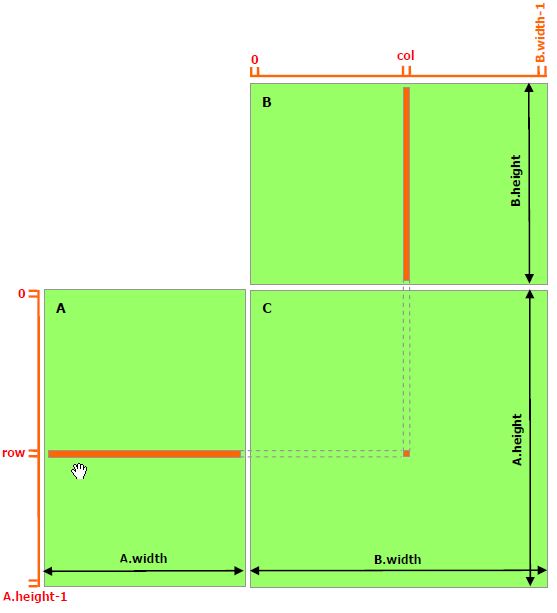
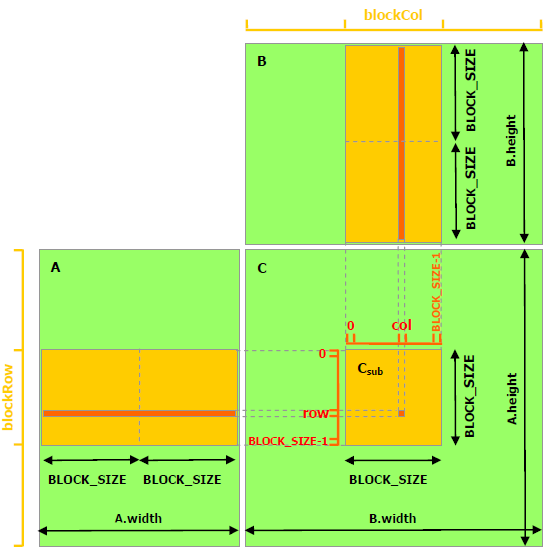
13.11. Example: matrix multiplication¶

[C] = [A] x [B]

Review and comparison:

Computing on the global memory.
Computing on the shared memory.

_images/matrix-multiplication-without-shared-memory.png

13.12. Thread computing on the `global memory`.¶

// Matrices are stored in row-major order:
// M(row, col) = *(M.elements + row * M.width + col)
typedef struct {
    int width;
    int height;
    float* elements;
} Matrix;

// Thread block size
#define BLOCK_SIZE 16

// Forward declaration of the matrix multiplication kernel
__global__ void MatMulKernel(const Matrix, const Matrix, Matrix);

// Matrix multiplication - Host code
// Matrix dimensions are assumed to be multiples of BLOCK_SIZE
void MatMul(const Matrix A, const Matrix B, Matrix C)
{

    // Load A and B to device memory
    Matrix d_A;
    d_A.width = A.width; d_A.height = A.height;
    size_t size = A.width * A.height * sizeof(float);
    cudaMalloc(&d_A.elements, size);
    cudaMemcpy(d_A.elements, A.elements, size, cudaMemcpyHostToDevice);
    Matrix d_B;
    d_B.width = B.width; d_B.height = B.height;
    size = B.width * B.height * sizeof(float);
    cudaMalloc(&d_B.elements, size);
    cudaMemcpy(d_B.elements, B.elements, size, cudaMemcpyHostToDevice);

    // Allocate C in device memory
    Matrix d_C;
    d_C.width = C.width; d_C.height = C.height;
    size = C.width * C.height * sizeof(float);
    cudaMalloc(&d_C.elements, size);

    // Invoke kernel
    dim3 dimBlock(BLOCK_SIZE, BLOCK_SIZE);
    dim3 dimGrid(B.width / dimBlock.x, A.height / dimBlock.y);
    
    MatMulKernel<<<dimGrid, dimBlock>>>(d_A, d_B, d_C);
   
    // Read C from device memory
    cudaMemcpy(C.elements, d_C.elements, size, cudaMemcpyDeviceToHost);

    // Free device memory
    cudaFree(d_A.elements);
    cudaFree(d_B.elements);
    cudaFree(d_C.elements);
}
// Matrix multiplication kernel called by MatMul()
__global__ void MatMulKernel(Matrix A, Matrix B, Matrix C)
{
    // Each thread computes one element of C
    // by accumulating results into Cvalue
    float Cvalue = 0;
    int row = blockIdx.y * blockDim.y + threadIdx.y;
    int col = blockIdx.x * blockDim.x + threadIdx.x;
    for (int e = 0; e < A.width; ++e)
      Cvalue += A.elements[row * A.width + e] * B.elements[e * B.width + col];
      C.elements[row * C.width + col] = Cvalue;
}

13.13. Computing with the `shared memory`¶

Threads in their own blocks compute the product on the submatrices, then copy the result into the global memory.

_images/matrix-multiplication-with-shared-memory.png

// Matrices are stored in row-major order:
// M(row, col) = *(M.elements + row * M.stride + col)
typedef struct {
    int width;
    int height;
    int stride; 
    float* elements;
} Matrix;

// Get a matrix element
__device__ float GetElement(const Matrix A, int row, int col)
{
    return A.elements[row * A.stride + col];
}

// Set a matrix element
__device__ void SetElement(Matrix A, int row, int col,
                           float value)
{
    A.elements[row * A.stride + col] = value;
}

// Get the BLOCK_SIZExBLOCK_SIZE sub-matrix Asub of A that is
// located col sub-matrices to the right and row sub-matrices down
// from the upper-left corner of A
 __device__ Matrix GetSubMatrix(Matrix A, int row, int col) 
{
    Matrix Asub;
    Asub.width    = BLOCK_SIZE;
    Asub.height   = BLOCK_SIZE;
    Asub.stride   = A.stride;
    Asub.elements = &A.elements[A.stride * BLOCK_SIZE * row
                                         + BLOCK_SIZE * col];
    return Asub;
}

// Thread block size
#define BLOCK_SIZE 16

// Forward declaration of the matrix multiplication kernel
__global__ void MatMulKernel(const Matrix, const Matrix, Matrix);

// Matrix multiplication - Host code
// Matrix dimensions are assumed to be multiples of BLOCK_SIZE
void MatMul(const Matrix A, const Matrix B, Matrix C)
{
    // Load A and B to device memory
    Matrix d_A;
    d_A.width = d_A.stride = A.width; d_A.height = A.height;
    size_t size = A.width * A.height * sizeof(float);
    cudaMalloc(&d_A.elements, size);
    cudaMemcpy(d_A.elements, A.elements, size, cudaMemcpyHostToDevice);
    Matrix d_B;
    d_B.width = d_B.stride = B.width; d_B.height = B.height;
    size = B.width * B.height * sizeof(float);
    cudaMalloc(&d_B.elements, size);
    cudaMemcpy(d_B.elements, B.elements, size, cudaMemcpyHostToDevice);

    // Allocate C in device memory
    Matrix d_C;
    d_C.width = d_C.stride = C.width; d_C.height = C.height;
    size = C.width * C.height * sizeof(float);
    cudaMalloc(&d_C.elements, size);

    // Invoke kernel
    dim3 dimBlock(BLOCK_SIZE, BLOCK_SIZE);
    dim3 dimGrid(B.width / dimBlock.x, A.height / dimBlock.y);
    MatMulKernel<<<dimGrid, dimBlock>>>(d_A, d_B, d_C);

    // Read C from device memory
    cudaMemcpy(C.elements, d_C.elements, size, cudaMemcpyDeviceToHost);

    // Free device memory
    cudaFree(d_A.elements);
    cudaFree(d_B.elements);
    cudaFree(d_C.elements);
}

// Matrix multiplication kernel called by MatMul()
 __global__ void MatMulKernel(Matrix A, Matrix B, Matrix C)
{
    // Block row and column
    int blockRow = blockIdx.y;
    int blockCol = blockIdx.x;

    // Each thread block computes one sub-matrix Csub of C
    Matrix Csub = GetSubMatrix(C, blockRow, blockCol);

    // Each thread computes one element of Csub
    // by accumulating results into Cvalue
    float Cvalue = 0;

    // Thread row and column within Csub
    int row = threadIdx.y;
    int col = threadIdx.x;

    // Loop over all the sub-matrices of A and B that are
    // required to compute Csub
    // Multiply each pair of sub-matrices together
    // and accumulate the results
    for (int m = 0; m < (A.width / BLOCK_SIZE); ++m) {

        // Get sub-matrix Asub of A
        Matrix Asub = GetSubMatrix(A, blockRow, m);

        // Get sub-matrix Bsub of B
        Matrix Bsub = GetSubMatrix(B, m, blockCol);

        // Shared memory used to store Asub and Bsub respectively
        __shared__ float As[BLOCK_SIZE][BLOCK_SIZE];
        __shared__ float Bs[BLOCK_SIZE][BLOCK_SIZE];

        // Load Asub and Bsub from device memory to shared memory
        // Each thread loads one element of each sub-matrix
        As[row][col] = GetElement(Asub, row, col);
        Bs[row][col] = GetElement(Bsub, row, col);

        // Synchronize to make sure the sub-matrices are loaded
        // before starting the computation
        __syncthreads();
        // Multiply Asub and Bsub together
        for (int e = 0; e < BLOCK_SIZE; ++e)
            Cvalue += As[row][e] * Bs[e][col];

        // Synchronize to make sure that the preceding
        // computation is done before loading two new
        // sub-matrices of A and B in the next iteration
        __syncthreads();
    }

    // Write Csub to device memory
    // Each thread writes one element
    SetElement(Csub, row, col, Cvalue);
}

13.14. Setup the environment for CUDA `nvcc` code compilation (Exercise)¶

CUDA 8.0 Toolkit is already installed on the lab desktops.
CUDA compiler, nvcc, depends on the GNU compilers it has been built with, gcc-5 and g+±5 in our case.
Install gcc-5 and g+±5 compilers:

apt install gcc-5
apt install g++-5

Make the installed compilers available as alternatives for gcc and g++:

update-alternatives --install /usr/bin/gcc gcc /usr/bin/gcc-5 5
update-alternatives --install /usr/bin/g++ g++ /usr/bin/g++-5 5

Set them as the default compilers:

update-alternatives --config gcc

select gcc-5

update-alternatives --config g++

select g++-5

Check if Linux on the desktop can communicate with the Nvidia GPU card,

nvidia-smi

If it shows the driver version and parameters in the output, skip the step and proceed to creating CUDA directory below. Otherwise, if it shows an error like NVIDIA-SMI has failed because it couldn’t communicate with the NVIDIA driver. Make sure that the latest NVIDIA driver is installed and running, rebuild the nvidia kernel module:

cd /usr/src/linux-headers-$(uname -r)
sudo make oldconfig && sudo make prepare # gnore the error
sudo dkms install nvidia/390.143
sudo modprobe nvidia
nvidia-smi

Create directory CUDA:

mkdir CUDA

Copy deviceQuery.cpp source code into directory CUDA, and compile it:

cd CUDA
cp  /usr/local/cuda/samples/1_Utilities/deviceQuery/deviceQuery.cpp .
nvcc -o deviceQuery deviceQuery.cpp -I /usr/local/cuda/samples/common/inc

Run the executable to see the prameters of the GPU card on your desktop:

./deviceQuery

13.15. Compile and run `hello.cu` (Exercise)¶

in directory CUDA, download a tar ball with cuda source codes, and extract the files:

wget http://linuxcourse.rutgers.edu/lessons/HPC_3/GPU.tgz
tar -zxvf GPU.tgz

Compile and run hello.cu:

nvcc -o hello hello.cu
./hello

Edit file hello.cu, and change the number of blocks to 4 and threads per block to 8 in the line that starts the device code:

print_from_gpu<<<4,8>>>();

Recompile and run the code:

nvcc -o hello hello.cu
./hello

See how the output from the blocks and the threads changes.

13.16. Compile and run the matrix multiplication codes (Exercise)¶

A routine that computes the wallclock time for the device function has been added in the both matrix multiplication codes discussed above.

Compile and run the code with global memory computation:

nvcc -o matrix_mult  matrix_mult.cu 
./matrix_mult

Compile and run the code with shard memory computation:

nvcc -o matrix_mult_shared matrix_mult_shared.cu
./matrix_mult_shared

Compare the printed out wall clock times of the device part. Notice that matrix_mult_shared runs about 2.6 times faster than matrix_mult.

13.17. CUDA enabled programming environments¶

For example: Matlab and Python

CUDA support in Python comes in PyTorch, TensorFlow, pybind11, and pycuda.

13.18. Python programming environment: Jupyter notebook (Exercise)¶

Install Jupyter notebook on your desktop:

pip install notebook

Add the PATH environment variable in the bottom of .bashrc file in your home directory:

.bashrc

export PATH=$PATH:.local/bin

Source the .bashrc by running command:

source .bashrc

Assign the password to jupyter notes by running command:

jupyter notebook password

Start jupyter notes by command below:

jupyter notebook &

Access jupyter notebook through the browser on your virtual desktop by navigating to URL below:

jupyter

http://localhost:8888

Start a new python3 project in the jupyter notebook.

13.19. pycuda and scikit-cuda installation (Exercise)¶

On the desktop, install pycuda and scikit-cuda packages by running command:

pip install pycuda
pip install scikit-cuda

13.20. Matrix multiplication (Exercise)¶

In your Jupyter notebook, copy and paste the python code from the cell below:

#Matrix multiplication:
import pycuda.gpuarray as gpuarray
import numpy as np
import skcuda.linalg as linalg

# --- Initializations
import pycuda.autoinit
linalg.init()

A = np.array(([1, 2, 3], [4, 5, 6])).astype(np.float64)
B = np.array(([7, 8, 1, 5], [9, 10, 0, 9], [11, 12, 5, 5])).astype(np.float64)

A_gpu = gpuarray.to_gpu(A)
B_gpu = gpuarray.to_gpu(B)

C_gpu = linalg.dot(A_gpu, B_gpu)

print(np.dot(A, B)) # compare with numpy result on the host
print(C_gpu)

Press <shift>-<Enter> keys to execute the script in the jupyter cell.

13.21. Matrix transposition (Exercise)¶

In your Jupyter notebook, copy and paste the python code from the cell below:

#Matrix transposition
import pycuda.autoinit
import pycuda.driver as drv
import pycuda.gpuarray as gpuarray
import numpy as np
import skcuda.linalg as linalg
linalg.init()
a = np.array([[1, 2, 3, 4, 5, 6], [7, 8, 9, 10, 11, 12]], np.float32)
a_gpu = gpuarray.to_gpu(a)
at_gpu = linalg.transpose(a_gpu)
print(at_gpu)
np.all(a.T == at_gpu.get()) # compare with numpy result on the host

Press <shift>-<Enter> keys to execute the script in the jupyter cell.

13.22. Eigenvalues and eigenvectors (Exercise)¶

In your Jupyter notebook, copy and paste the python code from the cell below:

# Eigenvalues and eigenvectors:
import pycuda.gpuarray as gpuarray
import pycuda.autoinit
import numpy as np
from skcuda import linalg
linalg.init()
a = np.array(([1,3,8],[3,5,17],[7,3,9]), np.float32, order='F')
a_gpu = gpuarray.to_gpu(a)
vr_gpu, w_gpu = linalg.eig(a_gpu, 'N', 'V')
print('Eigenvalues: ', w_gpu) #eigenvalues
print('Eigenvectors: ', vr_gpu) #eigenvectors

Press <shift>-<Enter> keys to execute the script in the jupyter cell.

13.23. References¶

CUDA C++ Programming Guide by Nvidia

scikit-cuda library reference

numpy tutorial

Computing Environment

13. Introduction to GPU computing with CUDA¶

13.1. HOW GPU accelerated computing works¶

13.2. Type of compute tasks to run on GPU¶

13.3. Applications runnable on GPU¶

13.4. GPU computing cons and pros¶

13.5. Host and Device parts of a code¶

13.6. Threads, blocks, warps, and grid¶

13.7. Blocks on Streaming Multiprocessors (SM)¶

13.8. Thread indexing¶

13.9. Memory Hierarchy¶

13.10. The main challenge in CUDA computing is memory management¶

13.11. Example: matrix multiplication¶

13.12. Thread computing on the global memory.¶

13.13. Computing with the shared memory¶

13.14. Setup the environment for CUDA nvcc code compilation (Exercise)¶

13.15. Compile and run hello.cu (Exercise)¶

13.16. Compile and run the matrix multiplication codes (Exercise)¶

13.17. CUDA enabled programming environments¶

13.18. Python programming environment: Jupyter notebook (Exercise)¶

13.19. pycuda and scikit-cuda installation (Exercise)¶

13.20. Matrix multiplication (Exercise)¶

13.21. Matrix transposition (Exercise)¶

13.22. Eigenvalues and eigenvectors (Exercise)¶

13.23. References¶

13.12. Thread computing on the `global memory`.¶

13.13. Computing with the `shared memory`¶

13.14. Setup the environment for CUDA `nvcc` code compilation (Exercise)¶

13.15. Compile and run `hello.cu` (Exercise)¶