- Presto, Innate Forms: Background

Patterns in natural systems abound, from the stripes on a zebra to ripples in a riverbed.  In many of these systems, the appearance of an ordered state is not unexpected as the outcome of an underlying ordered process.  Thus crystal growth, honeycomb manufacture and floret evolution generate regular and predictable patterns.  Surprisingly similar patterns are generated by intrinsically noisy and disordered processes such as thermal fluctuations or mechanically randomized scattering.  In this work, we examine some of the underlying mechanisms believed to be at the heart of these similarities.

- Note firm operants: The Second Law of Thermodynamics:

Maxwell's Demon is the paradigmatic thought experiment used to challenge the Second Law , and consists of the hypothetical process of extracting heat from a gas by opening an imaginary door separating two chambers only when high speed (i.e. hot) molecules approach the door from, say, the right.   A meticulous analysis of the actual energy required to implement such a machine reveals that the Second Law is sound because the minimum expenditure of energy needed to detect and respond to fast particles is nonzero and in fact exactly equals that predicted by quantitative forms of the Law [Caves et al., Phys. Rev. Lett 65 (1990) 1387].

In the case of granular physics, where much recent research on noise and pattern formation has focused, a surprising result is obtained however.  This result, first discussed  in 1996 [Schlichting et al., Math. Naturwiss. Unterr.  49 (1996), 323-332] and since analyzed in detail [Eggers, Phys. Rev. Lett. 83 (1999)  5322-5] , is epitomized in the figure below, where we display the results of an experiment in which a number of steel beads were initially uniformly distributed across a vibrated acrylic container.   The container is separated into two identical chambers by a foamboard barrier containing an open window near its bottom.

Granular Maxwell' s Demon (a) Snapshot of spontaneous separation between gas-like and solid-like 2 mm diameter steel balls from experiment in which a acrylic container is vibrated sinusoidally at 10 Hz and a maximum acceleration of 1.3 times gravity.  The beads are initially distributed uniformly across the container, and due to collisional inelasticity migrate to whichever side randomly acquires a slight excess of balls.  (b) Schematic of container which is divided into two chambers by a barrier containing a window 6 mm high beginning 6 mm from the bottom of the container.

- On a persistent form: Patterns from first order processes

Evidently and against expectation, ordering of large-scale particles into gas-like and frozen states can arise spontaneously.  The ingredients required to produce this outcome are a source of noisy energy (here the shaking of the container) and a source of dissipation (here the inelasticity of the particles).  The same ingredients on the micro-scale produce regular ordering in a variety of natural situations as well [Ball, The self-made tapestry, pattern formation in nature (Oxford U. Press, Oxford UK 1999)].  Historically, one of the earliest mentions of this kind of ordering -- and one of the most elegant systems in which it can be produced -- is the production of layered geological specimens, where 'Leisegang bands' of precipitating reactants can spontaneously form stripes and other patterns in otherwise static gels.

Ornament of stripes: Liesegang Bands Patterns in an Agar gel containing dissolved K2CrO4 to which CuSO4 has been added from above.  Details of this system suitable for instructional use appear at: Credit: Peter Garik, Matthew B. Gillespie & Kenneth Brecher, Mathematics Education Center, Boston University.

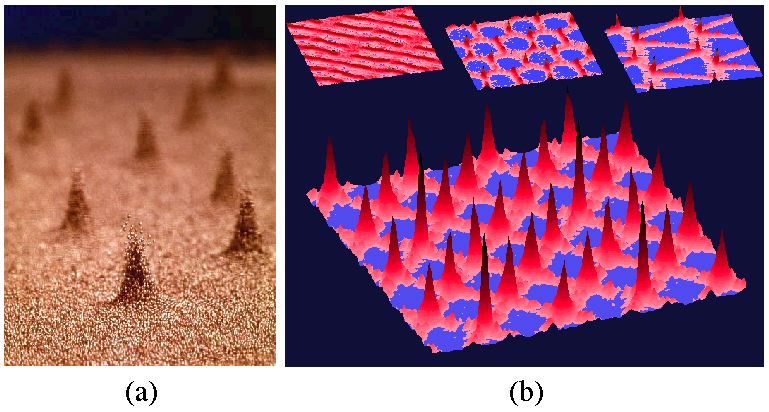
- Or tramp fine stones: Patterns from macroscale noise

Patterns are seen on all scales; from the microscopic to the astrophysical.  On laboratory scales, a variety of striking patterns have been reported, among the most intriguing of which are 'oscillons', consisting of a state of peaks and dips that alternate on successive vibration cycles .  An experimental example of an array of oscillons from Paul Umbanhowar and Harry Swinney is shown below, alongside a model that produces several other patterns, some of which are seen experimentally and one that has not been seen to date.

(a) Array of 'oscillons' from granular vibration experiment.  Credit: Paul Umbanhowar, Northwestern University and Harry L Swinney, University of Texas at Austin; (b) Patterns from simulations of 32767 idealized particles.

- Assent from protein: Liquid crystal patterns

Colloidal ordering has been known for many year to be governed by entropy .  This is important in a number of technological problems, including the generation of liquid crystal displays and the fabrication of polymer composites.  Intriguing examples in biological systems have also been found.  As an example, the figure below displays an intermediate stage in the kinetics of the isotropic­smectic transition of a polymer/virus mixture, from Zvonimir Dogic and Seth Fraden.

A tactoid of spontaneously aggregated rod-like viral particles.  Credit: Zvonimir Dogic and Seth Fraden, Brandeis University.

- A form is not present: When do disordered states occur?

Spontaneously organized patterns can be formed by combining little more than noise (or diffusion) with dissipation (or complex reactions) in a symmetric system.  Why is it, then, that in some problems a disordered, homogeneous state results, while in seemingly similar circumstances ordered, heterogeneous patterns appear?    On probabilistic grounds, one can conclude that the physically realized states that Nature chooses will correspond to the ones that maximize the number of possible particle rearrangements.  By counting all possible states, one finds that so-called 'entropic ordering' can favor either macroscopically heterogeneous or homogeneous states with a transition at calculable values of order parameters such as constituent concentrations.  Remarkably, states in which like particles separate can be strongly favored in randomized systems, and separated states can be enormously more probable than any mixed state.

This has long been known in colloidal and polymeric systems.  In granular physics, there are indications that entropic ordering may also govern segregation of dissimilar particles.   In the figure, below, we have vibrated a 5 mm deep blend of large (gold) and small (maroon) glass beads under identical conditions, but at three different sets of concentrations.  At high concentration of small beads (a), the small and large beads separate cleanly, each species favoring positions near walls.  As the relative concentration of small beads is reduced, the entropic advantage of mixing grows with respect to that of separation, and only a small region (bottom right of (b) of segregated small beads is seen.  Finally the entropy of the mixed state exceeds that of the homogeneous state, which finally prevails when the weight fraction of small beads in the bed drops below about 11% (c).

Possible granular transition between mixing and segregation of 1.8 mm (gold) and 0.8 mm (maroon) glass beads.  Vibration is approximately sinusoidal with peak acceleration 3.9 times gravity and frequency of 20 Hz. Under fixed conditions, the concentrations (as a weight fraction of the total granular bed) of small beads in the three snapshots are (a) 30%; (b) 12%;  (c) 11%.  Striped patterns, characteristic of vibrated grains, are evident in the figure but play no known role in the entropic segregation mechanism..

- Frontier Map Notes: Outlook

It has been said that any sufficiently advanced technology is indistinguishable from magic.  The inseparable facts that continue to attract researchers to the study of patterns generated from noise are that the mechanism for their formation is extremely basic, yet even once the mechanism has been thoroughly dissected and understood, its outcome still seems like magic.  The paradox that the spontaneous formation of these patterns seems to be simultaneously completely implausible and hugely probable is difficult to reconcile with a rational and systematic analysis of the natural world.  This situation has given rise to several unresolved, and possibly unresolvable, questions that are topics of ongoing research.